| Sommaire |
LES
NOMBRES
Dans ses
livres, Euclide a étudié les nombres,
et voici quelques réflexions sur ce sujet.
1)
La division Euclidienne
On doit à Euclide la première preuve de l’infinité
de l’ensemble des nombres premiers (nombre n’ayant aucun diviseur propre )
et de l’existence pour tout entier naturel au moins égal à 2, d’un
diviseur premier au moins inférieur à son carré, ce qui permet la recherche
de primarité. Un diviseur propre d’un nombre N est un diviseur non
trivial, c’est-à-dire distinct de 1 et de N.
Rappelons que, pour un mathématicien, une fraction doit avoir son numérateur
et son diviseur entiers puis, les Grecs ont effectué les quatre opérations sur
des rapports de grandeur comme le montre le livre 5 des Eléments. En
particulier les Grecs savaient calculer avec les nombres écrits sous forme
fractionnaire et qu’on nomme nombres rationnels.
Exemple : Dans la division Euclidienne de
38 par 3, le quotient est 12 et le reste est 2 :
38 = 3 x 12 + 2
2)
Ö2,
un nombre «inexprimable » pour les Grecs
Euclide a étudié ce nombre inexprimable
qu’est Ö2.
Voici ses propos :
« Pythagore affirme que a² + b² = c²
|
|
BC² = 2
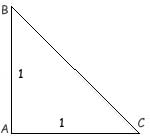 |
(1² = 1 et 2² = 4 …).
La rumeur court que ce nombre ne peut pas s’écrire
avec des nombres entiers, bref ! il est innommable …
Un homme se serait fait tuer pour avoir osé le
dire !
Il existe et on ne peut pas l’écrire… c’est
inconcevable … étudions-le :
Supposons tout de même que ce nombre soit
nommable ; soit a / b fraction simplifiée telle que
( a / b )² = 2.
a² / b² = 2 donc a² = 2b² … mais alors a² est
multiple de 2 donc pair d’où a est pair. a / b est simplifiée donc b est
impair c’est certain !
puisque a est pair, a = 2n donc a² = 4n².
a² = 2b² d’où 4n² = 2b², 2n² = b² … mais
alors b serait pair … je ne connais aucun nombre pair et impair ! !
Cette conclusion est absurde.
Tiens ! Ai-je aussi inventé le
raisonnement absurde ?
Car je dois conclure que mon hypothèse
initiale était fausse : le nombre dont le carré est 2, ne peut s’écrire
a / b ! ! ! Ce nombre n’est donc pas rationnel !
3) Le PGCD (Plus Grand Commun Diviseur à
Plus grand diviseur commun)
La
division euclidienne
Elle aussi porte mon nom … je n’en
demandais pas tant !
Divisez 17 par 5. Le quotient est 3 et le reste
est 2 (17 = 3 x 5 + 2 ). Les entiers, toujours eux ! Ils sont si rassurants !
Que de fois un architecte vient me voir pour des plans de temple : il connaît
déjà la longueur totale L de l’édifice, sa largeur l
mais veut placer des colonnes régulièrement espacées pour l’harmonie de
l’ensemble. J’ai donc mis au point un procédé (ont-ils compris ?)
pour trouver rapidement la distance entre 2 colonnes consécutives :
L = 777 coudées
l = 441 coudées
divisez 771 par 441
quotient 1
reste 336
divisez 441 par 336
quotient 1
reste 105
divisez 336 par 105
quotient 3
reste 21
divisez 105 par 21
quotient 6
reste 0
105 est donc multiple de 21. Vous placerez donc
vos colonnes toutes les 21 coudées. EvideMment vous pourrez les espacer
seulement de 3 ou 7 coudées … mais j’ai peur que ce soit un peut trop serré ! !
Qu’ai-je mis au point ? Le calcul du
PGCD de 2 nombres par la méthode «algorithme d’Euclide ». Encore moi ?
Oubliez-moi un peu …
Et pourtant cette technique ne fut pas facile
à justifier. Ils n’ont pas compris. Dommage !
Rappel
sur les nombres premiers
Rappelons ici que 2 nombres dont le PGCD est égal
à 1, sont dis premiers entre eux. Par exemple 35 et 12 sont premiers entre eux
et cependant aucun de ces nombres n’est premier puisque
12 = 3 x 4 et 35 = 5 x 7 !
On écrit
donc PGCD (12, 35 ) = 1
LE
NOMBRE D’OR
La proportion ø = (1 +
Ö5) / 2 »
1,618 033989 est depuis l'antiquité appelée et le nombre d'or elle
est considérée comme harmonieuse, belle et esthétique. La proportion du
nombre d'or et rencontrée en particulier en peinture et en architecture.